The beauty of compound interests
Introduction
Have you heard the Water lily’s enigma?
We have a lake on which we find a water lily the first day. The amount of water lily doubling every day, we find two water lilies on the second day. Knowing that after 50 days, the lac is entirely fulfilled with water lilies. How many days does it need for the lake to be half fulfilled?
The answer is obviously 49.
This enigma allows
The idea is really to understand that the previously realized gains will lead to an increase
Compound interests or simple interests?
There is two types of interests :
- Simple interest: these are the interests computed on the initially invested amount which are paid and therefore can be used by the investor once received.
- Compound interest: unlike the previous case, the interests are reinvested and are thus added to the invested amount on which the interests are computed. In this way, you do not directly benefit from the interests received meaning that you can’t use them to buy whatever you want but they will increase the capital on which the interests are computed.
The impact of compound interest in the short term can seem limited but the point is in the long term perspective where it can become really interesting.
Example of compound interests
Let’s take a numerical example to support what we just said :
We have a situation where a person A decides to invest 1.000 EUR each year at 10% interest rates on the compound interest plan while a second person B, using the same conditions, decides to use a simple interests plan. After 20 years, both of them will have invest 20.000 EUR.
However, as you can observe in the here below table, the situation of the two people is far from being similar. The simple interest method leads to annual interests of 21.000 EUR while the compound interest one brings this amount to 43.000 EUR, more than the double !

This example clearly establish the interest of compound interests which act in an exponential way. Please, find here below a graphic representation of the situation which highlight this exponential effect.

Therefore, the ideal would be to invest using the compound interest as soon as possible in order to benefit on the long term which will significantly increase your capital. I personally keep on the exercise here above to determine the amount of years needed to become a millionaire. After 48 years, you capital would be 1.056.189,57 EUR. Not so bad investing only 1.000 EUR each year.
However, it seems obvious that obtaining an interest rate of 10% without any risk is not that easy but this situation was only used as an example even though some peer-to-peer lending platforms offer such rate (such as the Mintos plateform)
Conclusion
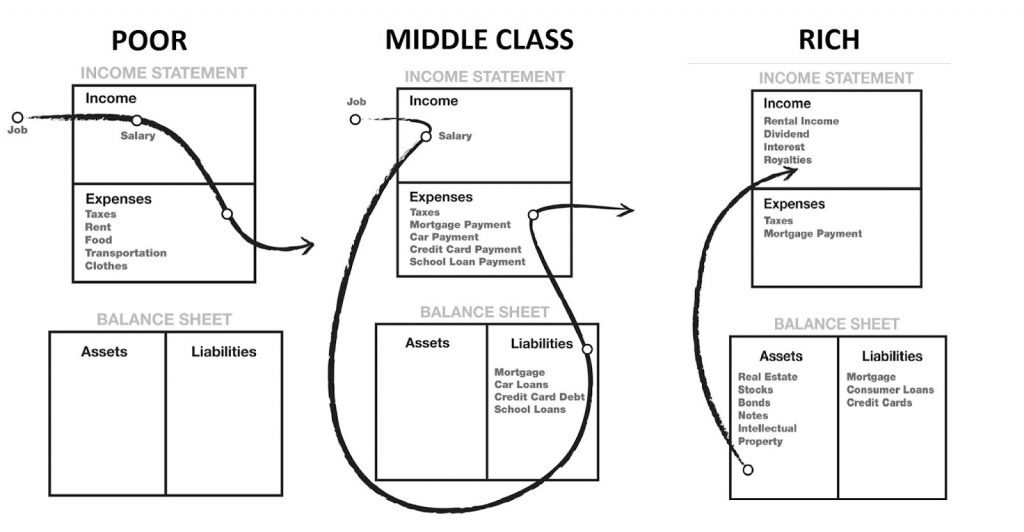
The general idea behind compound interests is to make your money work for you. As explained by Robert Kiyosaki in his book “Rich dad, poor dad”, “The rich do not work for money”. The latter would rather make their money work for them which can be done using compound interests. Those would allow you to generate cash while you sleep, isn’t it wonderful?